Improving the Safe Operation of Platoon Lane Changing for Connected Automated Vehicles: A Novel Field-Driven Approach
by Renfei Wu 1,2,3, Linheng Li 1,2,3, Wenqi Lu 1,2,3, Yikang Rui 1,2,3 and Bin Ran 1,2,3,*
from Appl. Sci. 2021, 11
Abstract
目前的研究主要集中在稳定性上缺少对变道的研究,本研究重点研究了队变道过程中的动态车距
建立了车队内车辆的车队内势场,可以有效表征车辆周围的风险分布。
设计了车队换道过程,分析了不同冲突情况下车队车辆的临界距离,究提出了车队变道临界距离模型。
最后,进行了实验,表明所提出的模型可以有效地表示队列中车辆之间的距离与周围车辆运动状态之间的关系。
Intro
变道研究可分为控制层面和策略层面:
控制层面:将变道作为统一的横向导航算法,期望的偏航率由偏航角跟踪控制器产生,然后通过操纵前轮实现变道
策略层面:在避免车辆碰撞的前提下,研究换道的时机和时机。
Zheng Z. Recent developments and research needs in modeling lane changing. Trans. Res. Part B 2014, 60, 16–32.
Schubert, R.; Schulze, K.; Wanielik, G. Situation assessment for automatic lane-change maneuvers. IEEE Trans. Intell. Transp.
Syst. 2010, 11, 607–616.
Wu, X.; Qiao, B.; Su, C. Trajectory planning with time-variant safety margin for autonomous vehicle lane change. Appl. Sci. 2020,
10, 1626.
非车队变道和车队变道有所不同,队列中的车辆由于其独特的协作特性,可以容忍更小的安全距离,但距离也不能过大,否则会导致高速场景中的队列解体。
另一种方法是在解散中进行队列变道。 如果在换道前或换道过程中解散队列,则车辆根据个别车辆的换道间隙逐一换道,然后所有车辆重新组成一个队列。 这种方法浪费了一个队列高效运输的优势,而且这个队列解散后通常无法重组。 由于高速公路上车辆行驶速度快,短时间内跟车和前车的状态会出现很大差异。
本文:
首次引入重力势场来表示队内车辆之间的牵引力;
引力势场和斥力势场统一为一个系统,命名为“队内势场”;
提出了队列变道安全间隔动态间隙的概念和计算方法;
提出了整队换道方法框架并进行了相关实验。
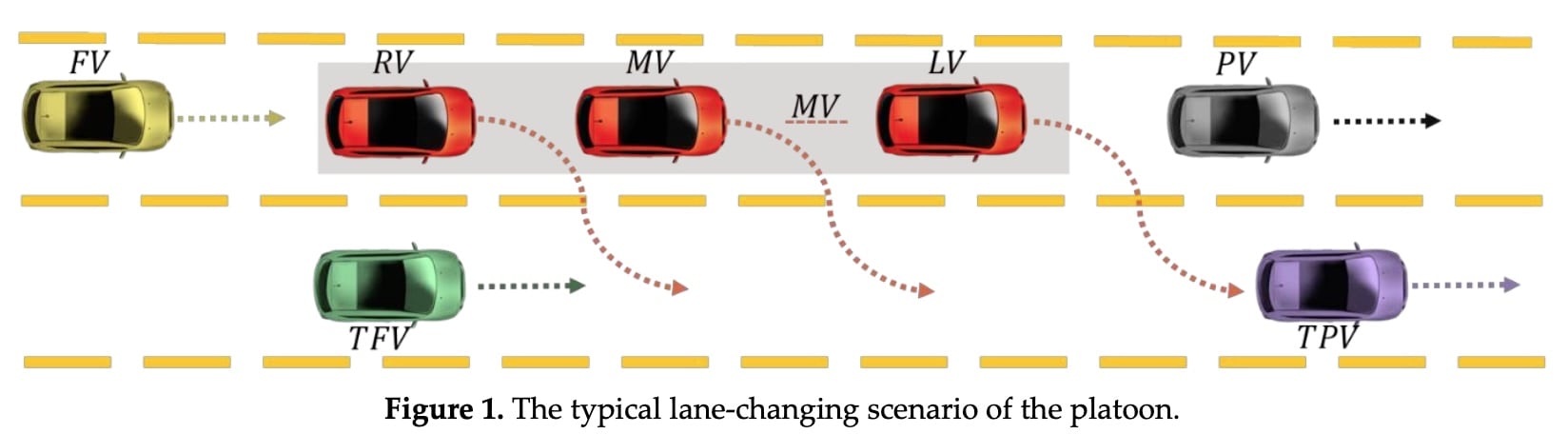
车队换道的定义
PV:preceding LV:leading MV:middle RV:rear FV:following
TFV: targert following, TPV:targert preceding
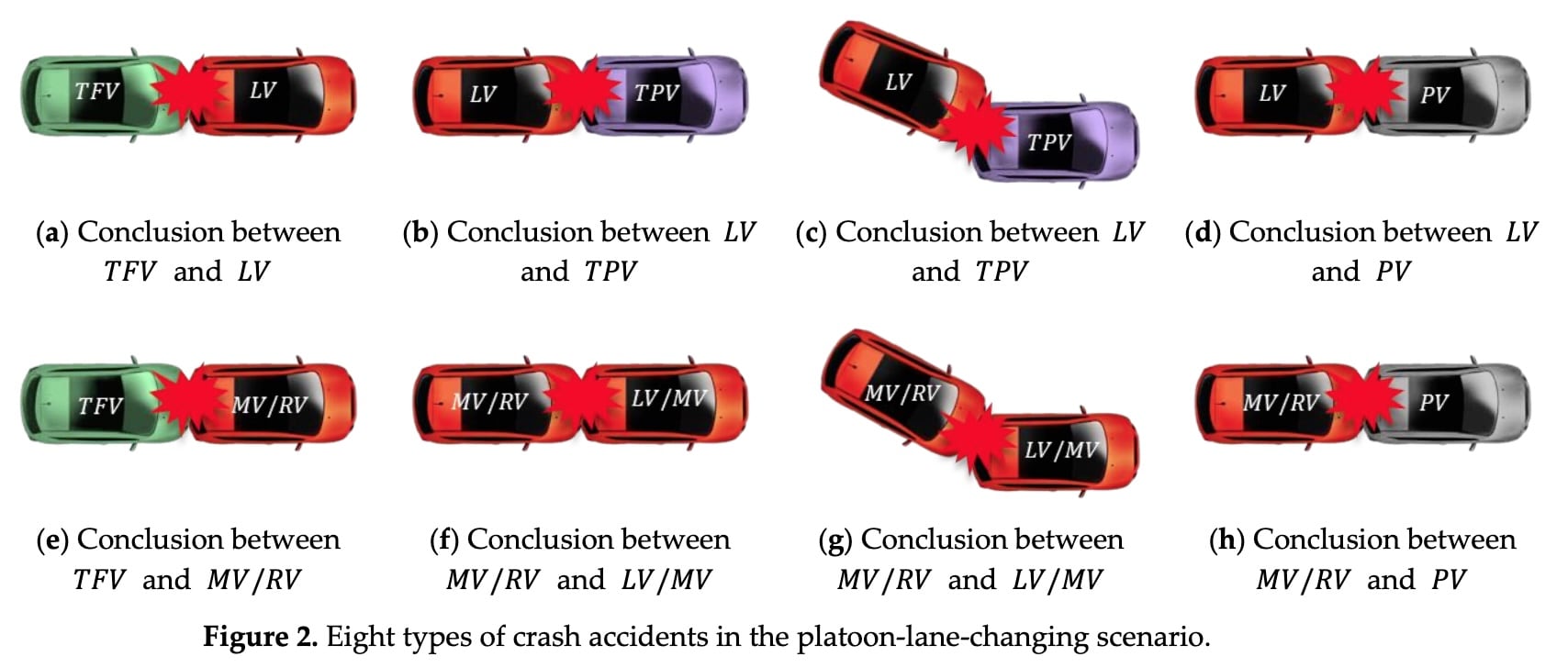
碰撞事故有多种类型,包括横向擦伤(scuffing)、侧面碰撞和追尾碰撞。当车队变道时,车队车辆与 𝑇𝐹𝑉/𝑇𝑃𝑉/𝑃𝑉 之间可能出现后两种碰撞形式,而对FV 几乎没有影响:
本研究的重点是避免图 f、g 中的两种冲突,这些冲突发生在队内车辆中。
队内势场法
队内势场(IPF)是一个物理场,表示复杂交通环境中目标之间风险的空间分布。目标是指可能发生碰撞或其当前状态可能导致重大损失的物体,例如车辆、行人和骑自行车的人。
判断换道行为能否成功的关键是本车与周围其他车辆保持安全距离,一个虚拟力作用在变道车辆上,使其改变运动状态,其中虚拟力由周围车辆提供。
E v = ( 1 2 ( E r + E g ) + c ) k ′ ∣ k ′ ∣ E_{v}=\left(\frac{1}{2}\left(E_{r}+E_{g}\right)+c\right) \frac{k^{\prime}}{\left|k^{\prime}\right|} E v = ( 2 1 ( E r + E g ) + c ) ∣ k ′ ∣ k ′ 其中𝐸𝑣代表队内势场,𝐸𝑟代表排斥势场,𝐸𝑔是引力势场,𝑐是与尺度校正相关的值。
E r = M i λ ⋅ e − β a i cos ∅ ∣ k ′ ∣ ⋅ k ′ ∣ k ′ ∣ E_{r}=M_{i} \lambda \cdot \frac{e^{-\beta a_{i} \cos \emptyset}}{\left|k^{\prime}\right|} \cdot \frac{k^{\prime}}{\left|k^{\prime}\right|} E r = M i λ ⋅ ∣ k ′ ∣ e − β a i c o s ∅ ⋅ ∣ k ′ ∣ k ′ E g = M i γ ∣ k ′ ∣ ⋅ e β a i cos ∅ ⋅ k ′ ∣ k ′ ∣ E_{g}=M_{i} \gamma\left|k^{\prime}\right| \cdot e^{\beta a_{i} \cos \emptyset} \cdot \frac{k^{\prime}}{\left|k^{\prime}\right|} E g = M i γ ∣ k ′ ∣ ⋅ e β a i c o s ∅ ⋅ ∣ k ′ ∣ k ′ ∣ k ′ ∣ = [ ( x ∗ − x e g o ) τ e α v i ] 2 + [ ( y ∗ − y e g o ) τ ] 2 \left|k^{\prime}\right|=\sqrt{\left[\left(x^{*}-x_{e g o}\right) \frac{\tau}{e^{\alpha v_{i}}}\right]^{2}+\left[\left(y^{*}-y_{e g o}\right) \tau\right]^{2}} ∣ k ′ ∣ = [ ( x ∗ − x e g o ) e α v i τ ] 2 + [ ( y ∗ − y e g o ) τ ] 2 M i = m i ( 1.566 × 1 0 − 14 v i 6.687 + 0.3345 ) M_{i}=m_{i}\left(1.566 \times 10^{-14} v_{i}^{6.687}+0.3345\right) M i = m i ( 1.566 × 1 0 − 14 v i 6.687 + 0.3345 ) 𝑀𝑖 是等效质量,𝑘'是指虚拟距离以提供自我车辆速度𝑣与势场强度之间的关系。∅ 是任一点与自车速度方向的顺时针夹角,𝜆 和 𝛽 分别是与等效质量和顺时针夹角相关的待定参数。
车辆变道与跟车有本质区别,但变道开始和结束时的临界状态是跟车状态。
但由于车辆在变道过程中存在斜向运动,很难保持固定距离,无法用车头时距公式计算。 两车之间的距离会在最佳距离上下波动,形成一个距离区间。根据本研究中最佳距离的定义,选择 1.4 s 作为期望的车头时距,以校准换道过程开始时的最佳距离。
在 IPF 中,场轮廓有一个最小环。 当本车的最小环与前车的最小环相切时,两车之间的距离就是物理意义上的最优距离。
D = k e + k f D=k_{e}+k_{f} D = k e + k f { k e = λ e α v e + β a e γ ⋅ τ k f = λ e α v f + β a f γ ⋅ τ \left\{\begin{array}{l}
k_{e}=\frac{\sqrt{\lambda} e^{\alpha v_{e}+\beta a_{e}}}{\sqrt{\gamma} \cdot \tau} \\
k_{f}=\frac{\sqrt{\lambda} e^{\alpha v_{f}+\beta a_{f}}}{\sqrt{\gamma} \cdot \tau}
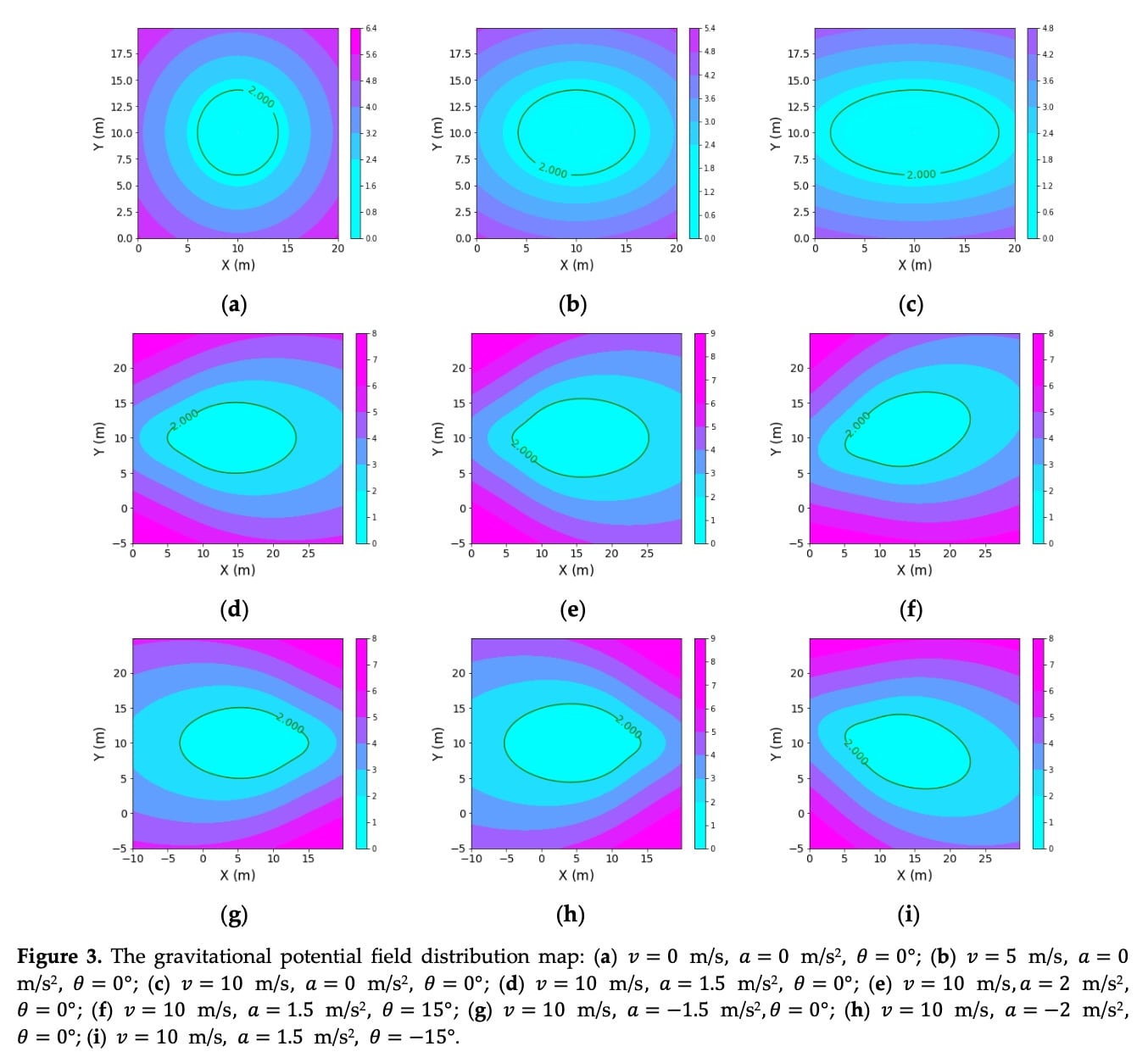
\end{array}\right. { k e = γ ⋅ τ λ e α v e + β a e k f = γ ⋅ τ λ e α v f + β a f 该模型可以动态反馈车队车辆在不同运动状态下的重力势场分布。 生成风险图,如下图所示。绿色等高线表示将具有相同势场的点投影到平面上形成的水平曲线。 从青色到紫色的颜色表示势场的强度。 当某一点的颜色越接近紫色时,表明引力势场的值越大,即引力惩罚越大。 相反,颜色越接近青色,引力损失越小。
不同临界条件下的临界安全距离
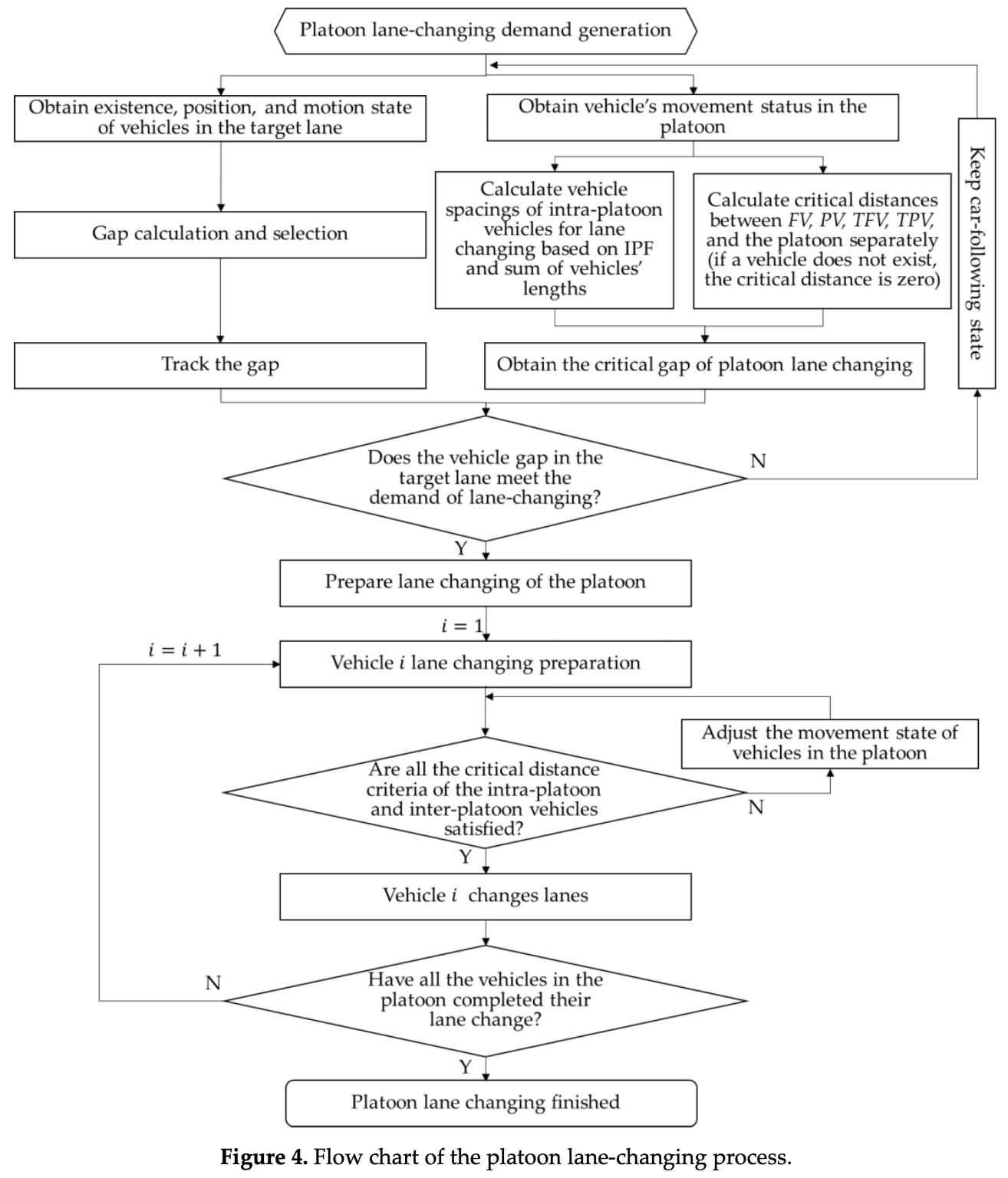
本节讨论了车队变道流程图的设计和临界安全距离建模。
如果答案是“N”,则排将保持跟车状态,直到找到合适的间隙。 一旦目标车道中的间隙满足临界间隙标准,车队将首先准备使用𝐿𝑉进行换道。
𝐿𝑉完成换道后,后续车辆将以同样的方式判断、调整并完成换道,直到所有本车在变道时可能会与目标车道上的前方车辆发生碰撞。 根据两车的运动状态,两车在变道场景下的IPF分布如图5所示车完成换道任务。
避免追尾的安全距离阈值
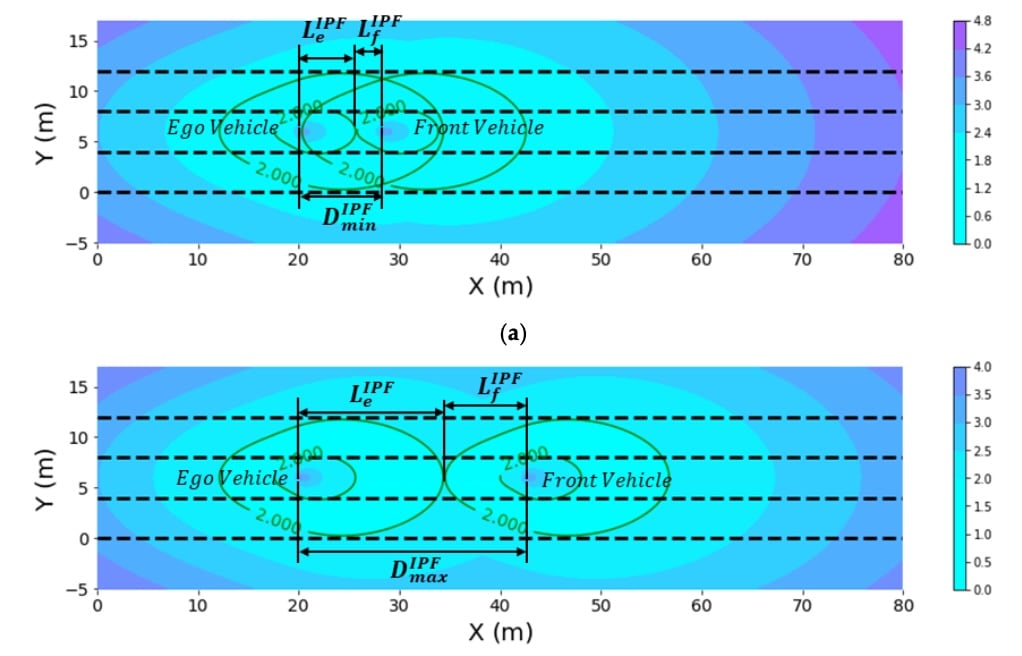
本车在变道时可能会与目标车道上的前方车辆发生碰撞。 根据两车的运动状态,两车在变道场景下的IPF分布如下图所示:
其中有两个临界场景。 图5a中两车场值分布的内圈相切,图5b中真实场值 real field values 分布的外圈相切。
在图5a中内圆相切的场景中,可以理解为保证本车在变道过程中和变道后避免与前车发生碰撞,本车与本车之间的最小车头时距 前车应该大于𝐷𝑚𝑖𝑛。 其公式如下:
D min = D min I P F − L e 2 + L f 2 D_{\min }=D_{\min }^{I P F}-\frac{L_{\mathrm{e}}}{2}+\frac{L_{f}}{2} D m i n = D m i n I PF − 2 L e + 2 L f D m i n I P F = L e I P F + L f I P F L e I P F = 1 2 M i γ τ ⋅ e − β a e cos θ e + α v e ⋅ ( − E v 2 − 4 M i 2 λ γ + E v ) L f I P F = 1 2 M i γ τ ⋅ e − β a f + α v f ⋅ ( − E v 2 − 4 M i 2 λ γ + E v ) \begin{gathered}
D_{m i n}^{I P F}=L_{e}^{I P F}+L_{f}^{I P F} \\
L_{e}^{I P F}=\frac{1}{2} M_{i} \gamma \tau \cdot e^{-\beta a_{e} \cos \theta_{e}+\alpha v_{e}} \cdot\left(-\sqrt{E_{v}{ }^{2}-4 M_{i}{ }^{2} \lambda \gamma}+E_{v}\right) \\
L_{f}^{I P F}=\frac{1}{2} M_{i} \gamma \tau \cdot e^{-\beta a_{f}+\alpha v_{f}} \cdot\left(-\sqrt{E_{v}{ }^{2}-4 M_{i}{ }^{2} \lambda \gamma}+E_{v}\right)
\end{gathered} D min I PF = L e I PF + L f I PF L e I PF = 2 1 M i γ τ ⋅ e − β a e c o s θ e + α v e ⋅ ( − E v 2 − 4 M i 2 λγ + E v ) L f I PF = 2 1 M i γ τ ⋅ e − β a f + α v f ⋅ ( − E v 2 − 4 M i 2 λγ + E v ) L 是车长,在图 5b 中,外圆相互相切,可以理解为确保两车之间的距离不会过大,影响排的稳定性,ego 之间的最大距离 变道过程中车辆与前车的距离应小于𝐷𝑚𝑎𝑥;
D max = D max I P F − L e 2 + L f 2 D max I P F = L e I P F + L f I P F L e I P F = 1 2 M i γ τ ⋅ e − β a e cos θ e + α v e ⋅ ( E v 2 − 4 M i 2 λ γ + E v ) L f I P F = 1 2 M i γ τ ⋅ e − β a f + α v f ⋅ ( E v 2 − 4 M i 2 λ γ + E v ) \begin{gathered}
D_{\max }=D_{\max }^{I P F}-\frac{L_{\mathrm{e}}}{2}+\frac{L_{f}}{2} \\
D_{\max }^{I P F}=L_{e}^{I P F}+L_{f}^{I P F} \\
L_{e}^{I P F}=\frac{1}{2} M_{i} \gamma \tau \cdot e^{-\beta a_{e} \cos \theta_{e}+\alpha v_{e}} \cdot\left(\sqrt{E_{v}{ }^{2}-4 M_{i}{ }^{2} \lambda \gamma}+E_{v}\right) \\
L_{f}^{I P F}=\frac{1}{2} M_{i} \gamma \tau \cdot e^{-\beta a_{f}+\alpha v_{f}} \cdot\left(\sqrt{E_{v}{ }^{2}-4 M_{i}{ }^{2} \lambda \gamma}+E_{v}\right)
\end{gathered} D m a x = D m a x I PF − 2 L e + 2 L f D m a x I PF = L e I PF + L f I PF L e I PF = 2 1 M i γ τ ⋅ e − β a e c o s θ e + α v e ⋅ ( E v 2 − 4 M i 2 λγ + E v ) L f I PF = 2 1 M i γ τ ⋅ e − β a f + α v f ⋅ ( E v 2 − 4 M i 2 λγ + E v ) 避免侧面碰撞的安全距离阈值
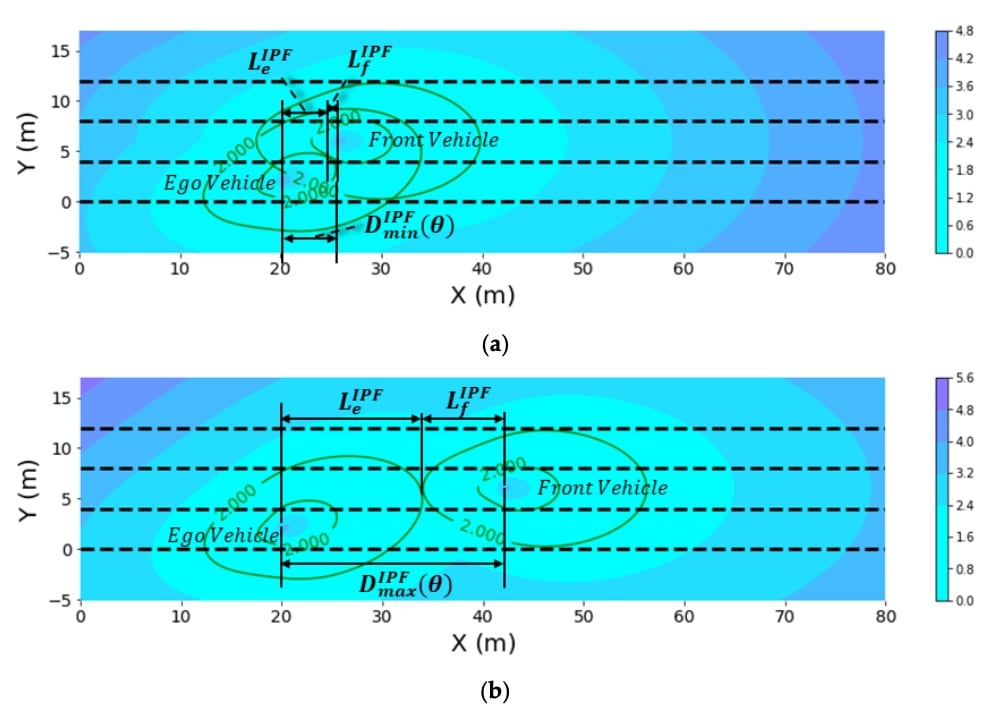
为保证本车在变道过程中和变道后不与前车发生碰撞,本车与前车的最小车头时距应为 大于𝐷𝑚𝑖𝑛(𝜃):
D min ( θ ) = D min I P F − L e 2 ⋅ cos θ + L f ^ 2 D_{\min }(\theta)=D_{\min }^{I P F}-\frac{L_{\mathrm{e}}}{2} \cdot \cos \theta+\frac{L_{\hat{f}}}{2} D m i n ( θ ) = D m i n I PF − 2 L e ⋅ cos θ + 2 L f ^ D min A P F ( θ ) = L e I P F ⋅ cos θ + L f ^ I P F L e I P F = 1 2 M i γ τ ⋅ e − β a e cos θ e + α v e ⋅ ( − E v 2 − 4 M i 2 λ γ + E v ) L f ^ I P F = 1 2 M i γ τ ⋅ e − β a f ^ + α v f ^ ⋅ ( − E v 2 − 4 M i 2 λ γ + E v ) \begin{gathered}
D_{\min }^{A P F}(\theta)=L_{e}^{I P F} \cdot \cos \theta+L_{\hat{f}}^{I P F} \\
L_{e}^{I P F}=\frac{1}{2} M_{i} \gamma \tau \cdot e^{-\beta a_{e} \cos \theta_{e}+\alpha v_{e}} \cdot\left(-\sqrt{E_{v}{ }^{2}-4 M_{i}{ }^{2} \lambda \gamma}+E_{v}\right) \\
L_{\hat{f}}^{I P F}=\frac{1}{2} M_{i} \gamma \tau \cdot e^{-\beta a_{\hat{f}}+\alpha v_{\hat{f}}} \cdot\left(-\sqrt{E_{v}{ }^{2}-4 M_{i}{ }^{2} \lambda \gamma}+E_{v}\right)
\end{gathered} D m i n A PF ( θ ) = L e I PF ⋅ cos θ + L f ^ I PF L e I PF = 2 1 M i γ τ ⋅ e − β a e c o s θ e + α v e ⋅ ( − E v 2 − 4 M i 2 λγ + E v ) L f ^ I PF = 2 1 M i γ τ ⋅ e − β a f ^ + α v f ^ ⋅ ( − E v 2 − 4 M i 2 λγ + E v ) APF:车辆质心之间的最小纵向距离。
实验与讨论
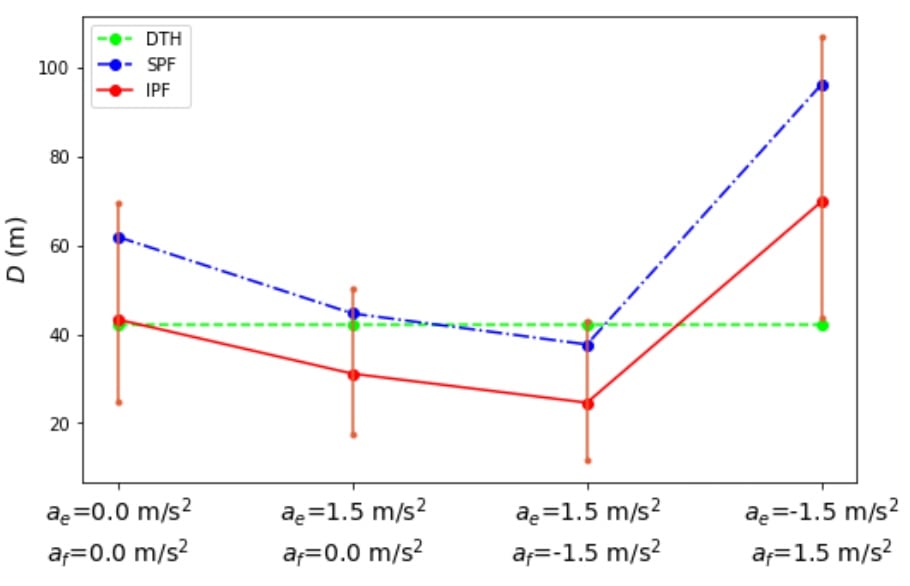
数值模拟分析结果,仿真过程中,本研究设置加速度取值范围为−2 m/s2 至 2 m/s2,转向角取值范围为 2° 至 5°。 还考虑了相关车辆的四种不同运动状态,即速度和加速度方面的四种不同运动状态组合。
所需车头时距 (DTH),对比安全势场 (SPF) 模型。