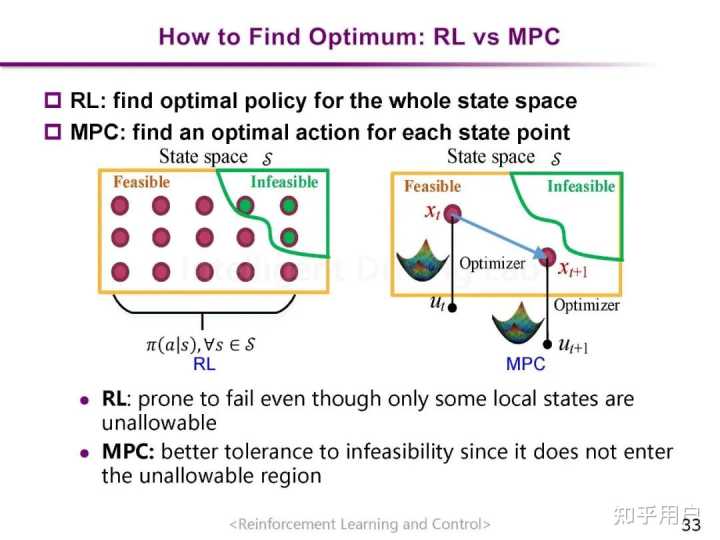
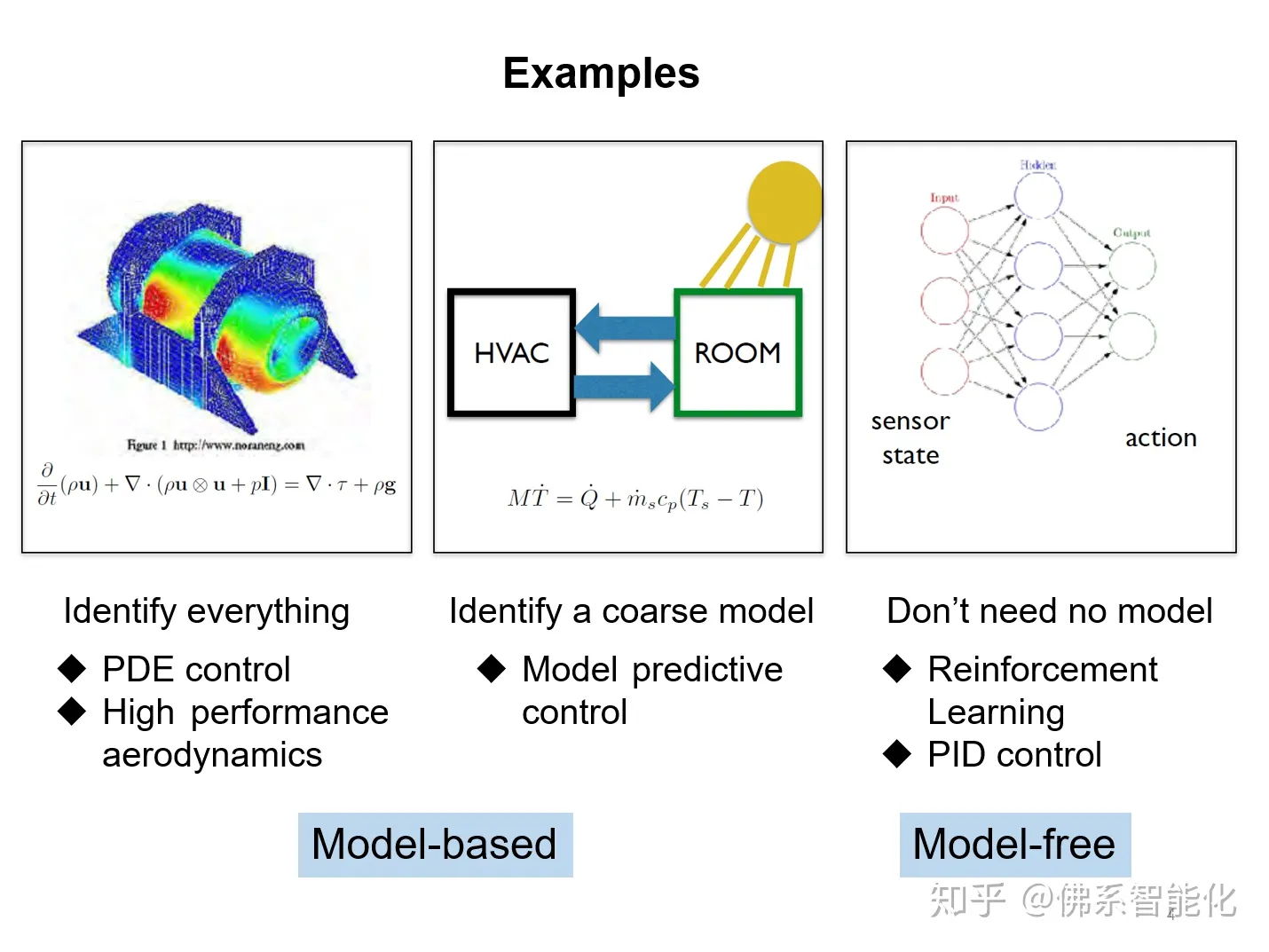
Latent Belief Space Motion Planning under Cost, Dynamics, and Intent Uncertainty | 在目标、动力学和意图不确定的隐含置信空间中进行无人车运动规划

公司网址：iSee.ai

by Qiu D, Zhao Y, Baker C L. 
from Robotics: Science and Systems. 2020.

Abstract

论文提出了一种新的轨迹规划与优化算法POMDPs（部分可观察的马尔可夫决策过程，Partially observable Markov decision processes），可以在连续空间（包括状态、动作及观测空间）中处理多模态（非正态分布）的不确定性。

与假设单峰高斯不确定性【unimodal Gaussian uncertainty】的先前信念空间运动规划【prior belief space motion planning approaches】方法不同，我们的方法构建了一种新的树结构表示可能的观察和多模式信念空间轨迹，并优化了该结构的应急计划（contingency plan）。

intro

首先是感知的不确定性，然后还有latent states （e.g. 下一个街区是否有空停车位，或者另一个司机是否打算让路）的不确定性。
需要平衡探索行动的成本与所获得信息的潜在收益。
部分可观察性下的规划问题，可以形式化为部分可观察的马尔可夫决策过程 (POMDP)，但是通常搞不定（intractable ）
轨迹优化技术非常有效，但通常需要状态完全可观察（或单独估计）
将轨迹优化扩展到置信空间规划，可以在适用于连续非线性机器人系统的运动规划算法中捕获部分可观察性。
目前的研究都是单峰，而现实世界的不确定性是多模态的（e.g. 旁车除了在位置和速度等状态上存在着服从正太分布的噪声，其驾驶者的性格也存在着另一层的离散型不确性）

问题建模

考虑离散时间，有限范围的POMDPs with 混合连续+离散的状态，连续的action 和 observation。

离散状态是动态且部分可观察的，这种状态的信念可以表示机器人状态的多模态、时变的不确定性。

其他agent 的连续状态假设完全可知的。

问题转化为一个 mixed-observability MDP model。

state space S = X × Z，X 为连续状态空间。

系统处于连续的状态-动作-观测空间中，而系统的状态转移除了受到上一时刻的状态和动作影响，还由一个离散的隐变量 $Z$ 决定.

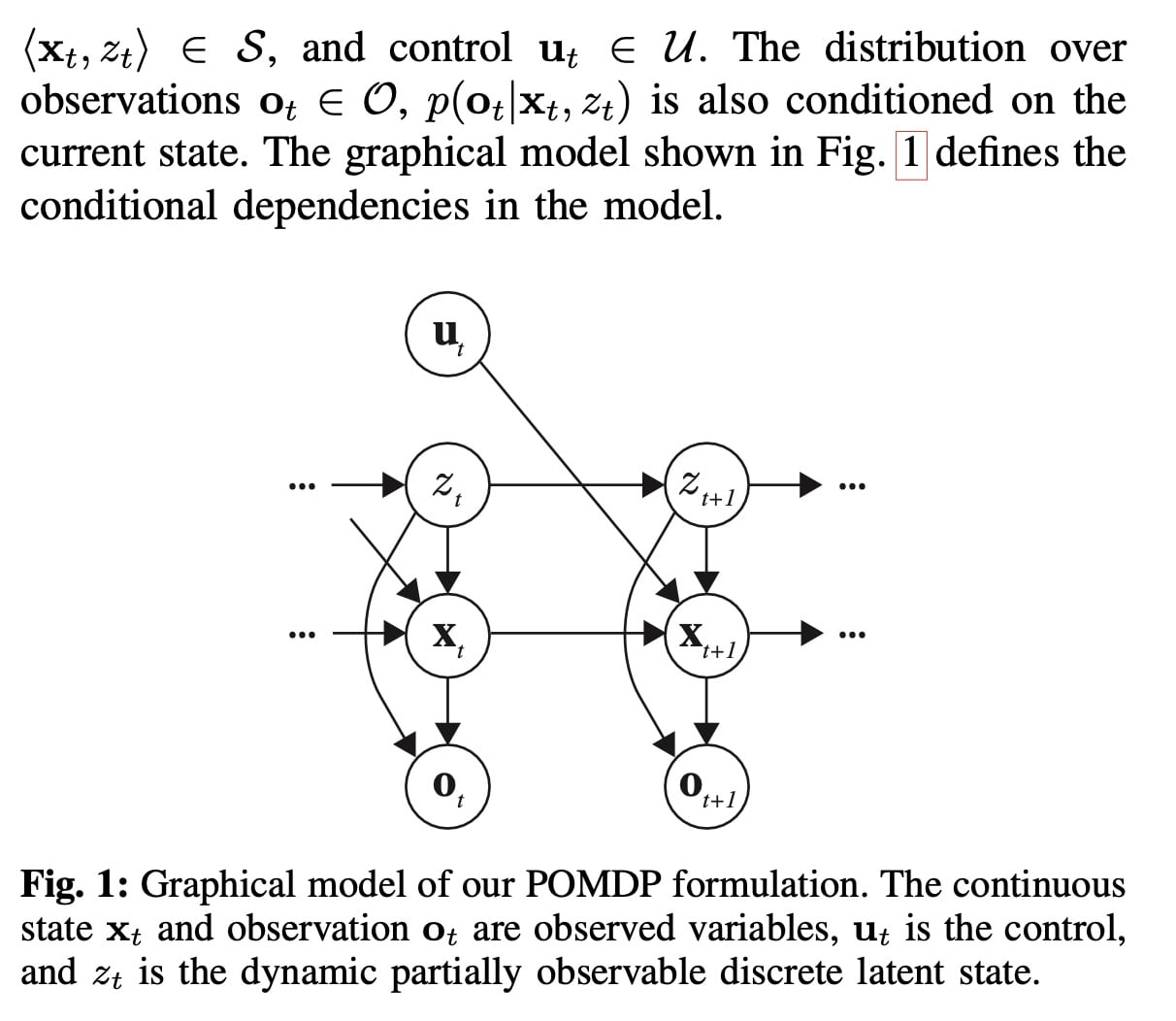
12染gwehbarnjyfdtmdu

使用递归贝叶斯过滤来更新隐变量：

\begin{aligned} \mathbf{b}_{t+1}\left(z_{t+1}\right) \triangleq & P\left(z_{t+1} \mid \mathbf{o}_{t+1}, \mathbf{x}_{t+1}, \mathbf{u}_t, \mathbf{x}_t, \ldots, \mathbf{o}_1, \mathbf{x}_1, \mathbf{u}_0, \mathbf{x}_0, \mathbf{b}_0\right) \\ =& P\left(z_{t+1} \mid \mathbf{o}_{t+1}, \mathbf{x}_{t+1}, \mathbf{x}_t, \mathbf{u}_t, \mathbf{b}_t\right) \\ =& \eta \cdot p\left(\mathbf{o}_{t+1} \mid \mathbf{x}_{t+1}, z_{t+1}\right) p\left(\mathbf{x}_{t+1} \mid z_{t+1}, \mathbf{x}_t, \mathbf{u}_t\right) \\ & \cdot \sum_{z_t \in \mathcal{Z}} P\left(z_{t+1} \mid z_t\right) \mathbf{b}_t(z) \end{aligned}

部分可观测微分动态规划（PODDP）

基于标准动态规划轨迹生成的最优化方法，例如DDP 和 iLQG，通过交替使用控制序列推出动力+成本的forward pass【看https://zhuanlan.zhihu.com/p/101129909 和 https://www.youtube.com/watch?v=4oDLMs11Exs】和采用局部二阶近似值的反向传递来优化轨迹函数，更新控制序列来优化这个近似值函数。重复此过程，直到收敛到局部最优轨迹。

PODDP 也把流程分为了前向过程（Forward Pass）和后向过程（Backward Pass），并对动作序列进行迭代优化。

向前过程

动作序列 U={ $u_0,u_1,⋯,u_{T−1}$ } 需要预先给定。一般使用随机生成的动作序列，或者通过前导知识有规律地生成动作序列。

在此后的过程中，将使用前一次优化得到的动作序列，进行迭代优化。

在确定性系统中，由于状态转移过程是确定的，故给定的动作序列将衍生出一条链式的状态序列。但由于多模态不确定性的存在，类比于离散空间下的 POMDP 问题，每一个节点都可以根据隐变量 z 的不同取值可能性，延伸出多个分支，最终形成一个树状的轨迹推演，即轨迹树（trajectory tree）

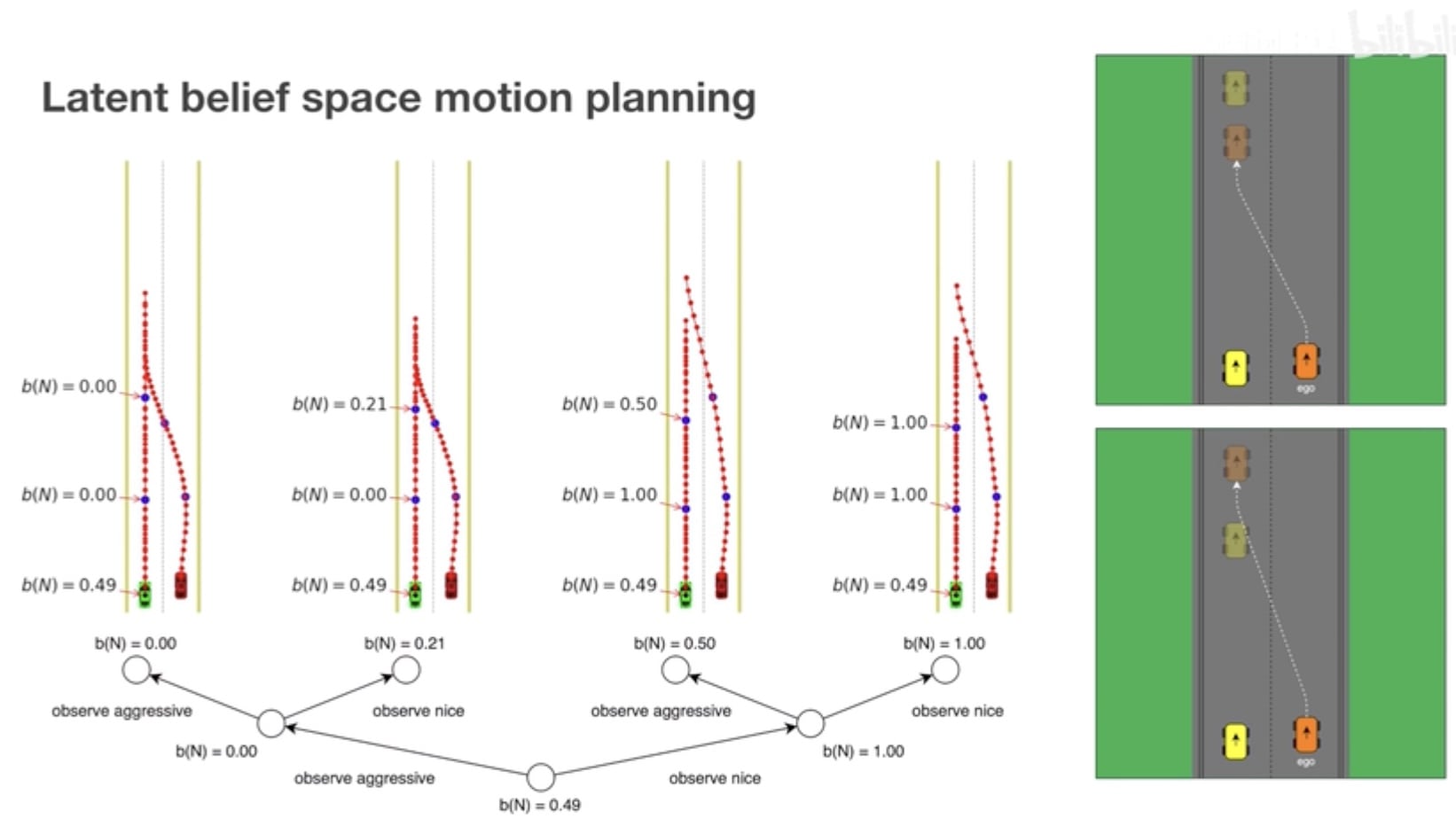
ytsgahdflsdk

后向过程

对轨迹树进行优化，在状态转换时不仅考虑系统状态 x 的演变，还考虑获得不同的观测值时置信度 b 的变化，通过置信度 b 进行加权平均，把后续分支节点进行合并。

实验结果

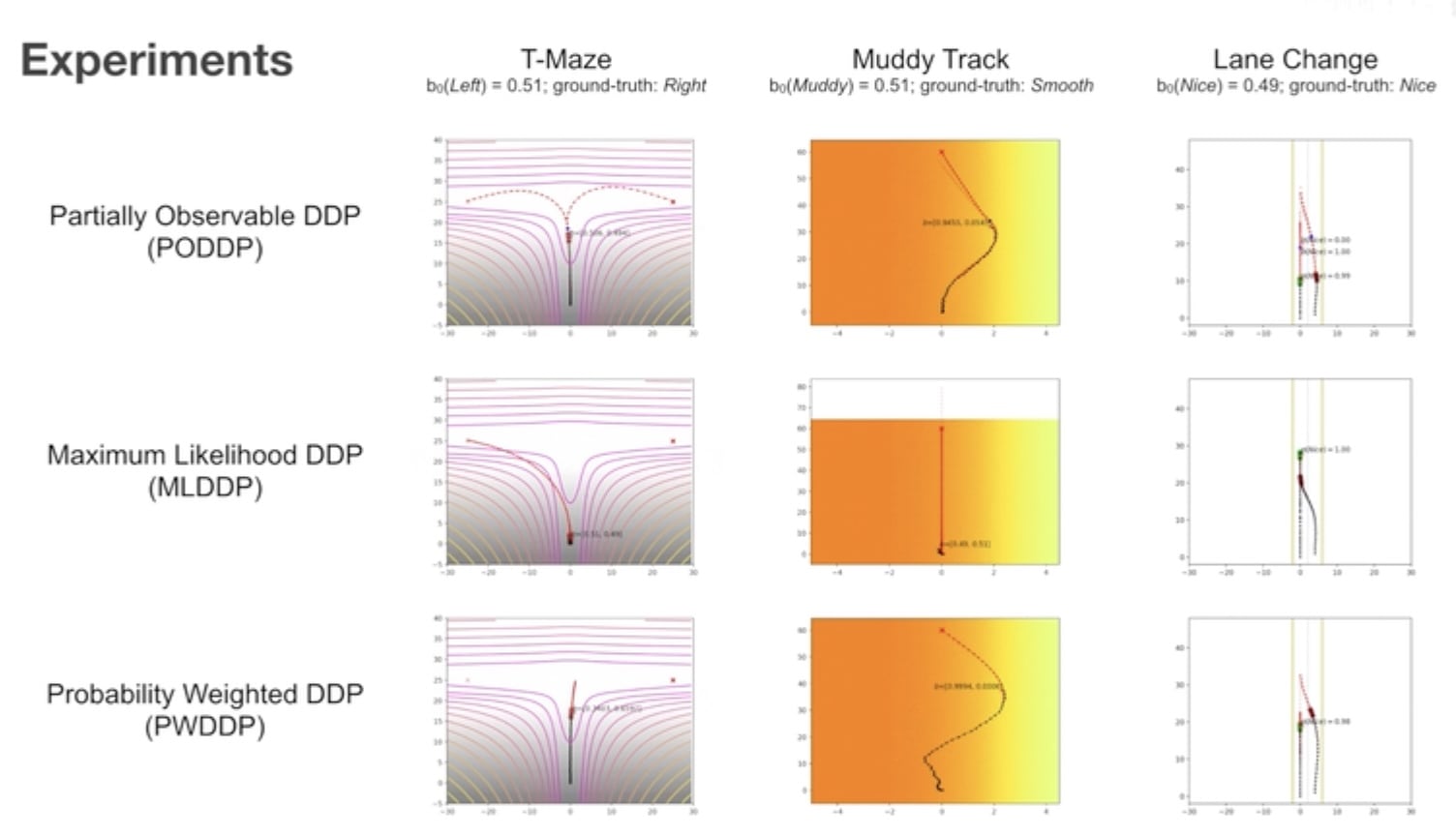
两种对照的 baseline 算法：

Probability Weighted DDP (PWDDP)：其根据当前时刻的置信度直接对所有可能性进行加权平均操作，而不考虑由于不同的未来观测值而产生的轨迹分支；
Maximum Likelihood DDP (MLDDP)：其只考虑当前时刻下置信度最高的隐变量，而忽略其他的可能性。

三类不确定性：

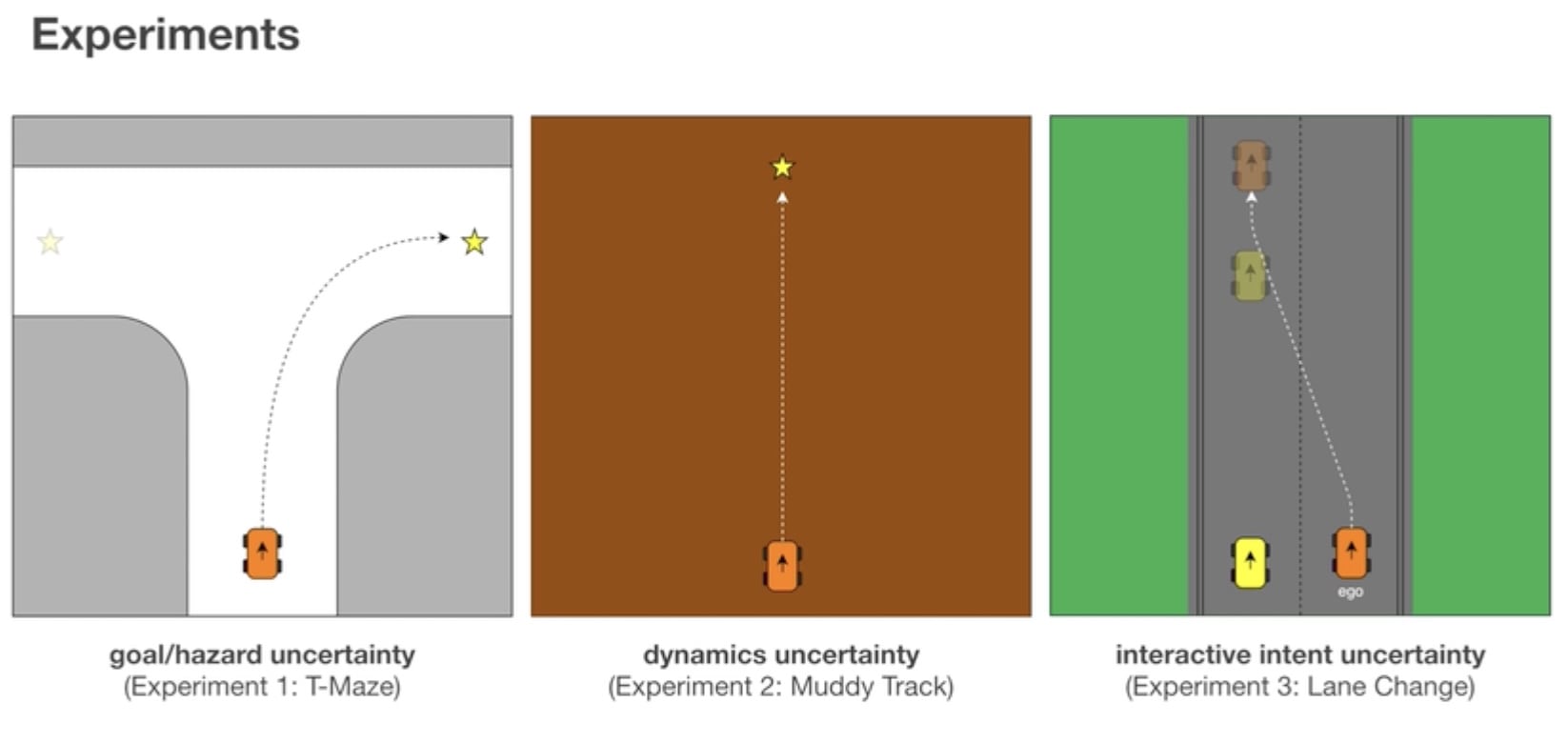
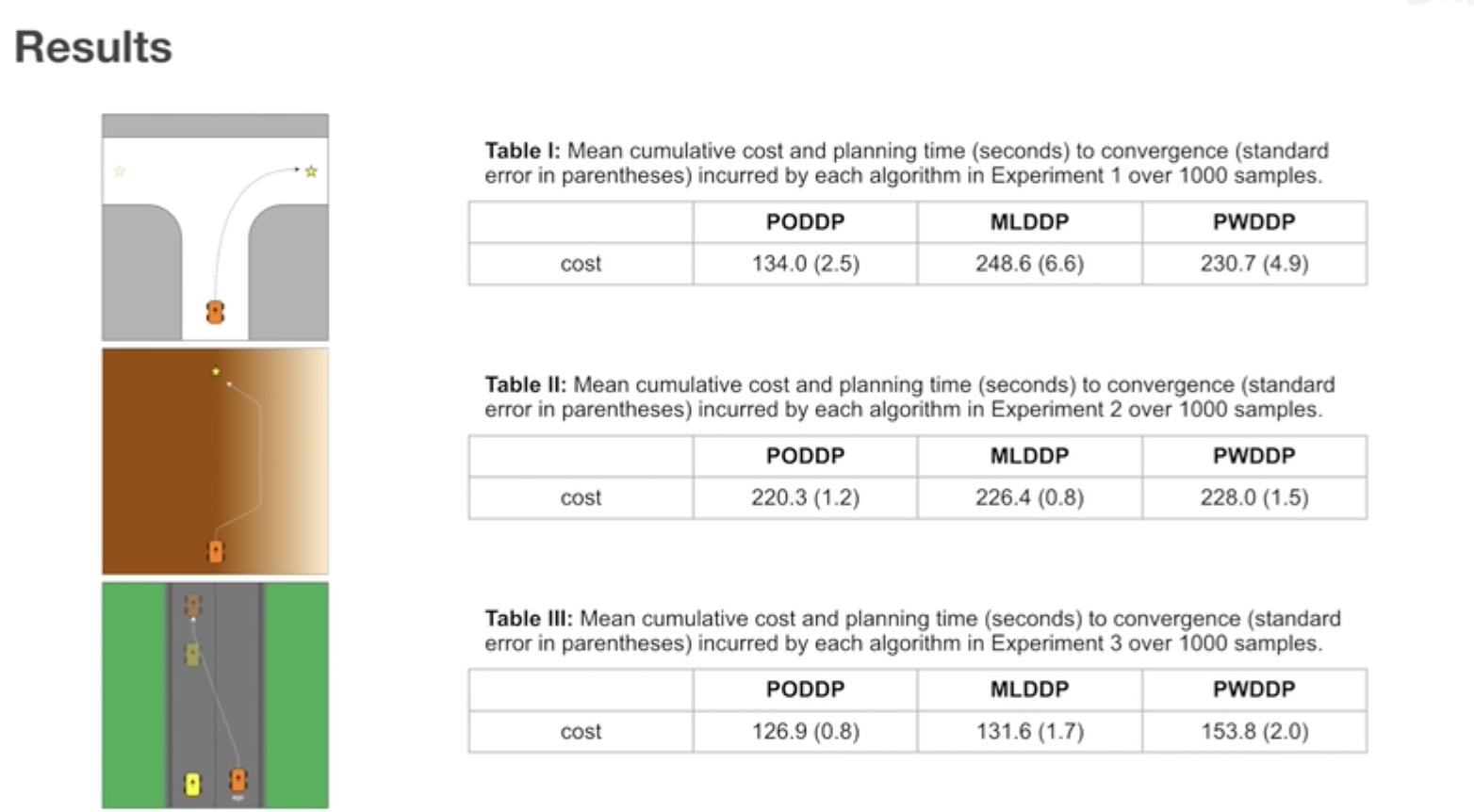
目标函数不确定（T-Maze 场景）：车辆位于一个T 字型的道路入口处，希望走到一个不确定的目标地点。该目标地点可能是道路的左侧，也可能是道路的右侧，而车辆必须沿侧道路行驶至靠近分叉口的地方才能够得到更好的观测，以确定目标所处的位置。
本体系统运动学规律不确定（Muddy Track 场景）：车辆在一条泥泞的道路上朝一个目标地点行驶，但右侧的道路有一定的可能性会更加平滑。而车辆必须在行驶中探索右侧道路是否真的更平滑，从而规划出一条最优的行进路线。
其他个体意图不确定（Lane Change 场景）：车辆希望并线到左侧车道，可是那里已经有另一辆车了。需要时刻评估对方是比较合作的，还是比较冲动激进的，进而确定应该超车并线，还是等待对方先向前走远再并线到它后方。

askdhaskj

akdhsakjdhau87697

asdisagiudgia13243

术语

freezing robot problem

Existing algorithms suffer from the “freezing robot” problem: once the environment surpasses a certain level of complexity, the planner decides that all forward paths are unsafe, and the robot freezes in place

DDP: Differential dynamic programming

强化学习和最优控制的关系

https://www.zhihu.com/question/401591393