Motion Planning under Uncertainty for On-Road Autonomous Driving

2014 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2014: 2507-2512.
by Wenda Xu, Jia Pan, Junqing Wei, and John M. Dolan

Abstract

What we did?

we develop a motion planning framework for autonomous on-road driving considering both the uncertainty caused by an autonomous vehicle and other traffic participants.

提出了一个规划框架，该框架能够同时考虑自动驾驶汽车和其他交通参与者造成的不确定性，以提高驾驶安全性。

How？

generate candidate trajectories based on a spatio-temporal lattice -> search for an optimal trajectory
uncertainty:
- autonomous vehicle -> Gaussian propagation :Linear-Quadratic Gaussian (LQG) framework
- other traffic participants -> estimate the control inputs they will choose using a local planner and then predict a distribution for their future states using a Kalman filter
  
  我们首先使用本地规划器估计他们将选择的控制输入，然后使用卡尔曼滤波器预测他们未来状态的分布，其中估计的控制输入和未来观察被用作输入

Advantage

Compared with other safety assessment methods, our framework allows the planner to avoid unsafe situations more efficiently, thanks to the direct uncertainty information feedback to the planner. We also demonstrate our planner’s ability to generate safer trajectories compared to planning only with a LQG framework.

Introduction

We first generate candidate trajectories based on a spatio-temporal lattice and then search for an optimal trajectory among them.

we consider the uncertainties caused by both

the autonomous vehicle itself : Linear-Quadratic Gaussian (LQG) framework + state measurement
other traffic participants : local input + Kalman filter

the quality of a candidate trajectory is evaluated based on a cost function related to the state distributions of both the candidate trajectory and other traffic participants.

Related work

A Partially Observable Markov Decision Process (POMDP) allows computing the control policy over the space of the belief state, which is a probability distribution over all the possible states. However, POMDP is known to be computationally expensive and scales poorly when the problem dimension increases.

LQG-based ( Linear-Quadratic Regulator ) -> more computational efficient but exclude the uncertainty due to the movement of dynamic obstacles.

可达集合障碍集是否重叠 -> 规划者不知道为什么这条轨迹是不安全的，这样的间接反馈可能无助于规划者找到安全的轨迹。

本文的贡献在于，我们提出了一种自动驾驶汽车的规划器，它不仅可以考虑自动驾驶汽车本身的不确定性，还可以考虑交通参与者的不确定性。

Uncertainty prediction of traffic participant

A. Vehicle Model

The future trajectories of traffic participants are determined by their current state and future control input

However, the future control inputs of traffic participants are unknown. motion primitives are first designed based on typical human driving behavior, and then they are evaluated using a cost function. Finally, the optimal motion primitive is chosen as the best estimation of this traffic participant’s future motion.

B. Gaussian Propagation

The vehicle dynamic model generally can be written or linearized as a time-varying linear model

Kalman filter

Uncertainty propagation for the autonomous vehicle

a LQR controller can be designed to track the planned trajectory
The tracking problem (ideal vs real) can be converted to a regulator problem

Trajectory planning

A. Trajectory Generation

通过使用三次曲率多项式连接相邻层中的端点来生成路径，路径的曲率是弧长的三次多项式。

B. Prediction for Traffic Participants

we make a simplified assumption that when we predict the motion for a traffic participant, all the other vehicles (including the autonomous vehicle) will keep moving with current speeds and have no uncertainty on their positions.

动态规划优化后的穷举来获取每个状态的最小成本

对于搜索阶段的每个轨迹，可以使用 LQG 框架计算状态沿轨迹的分布。

C. Planning for Autonomous Vehicle

D. Cost Function

1) Smoothness costs:

2) Static obstacle costs:

3) Dynamic obstacle costs:

Experimental results

自动驾驶汽车在左车道行驶，另一辆车在右车道行驶，第三辆汽车停在路边突出到右车道

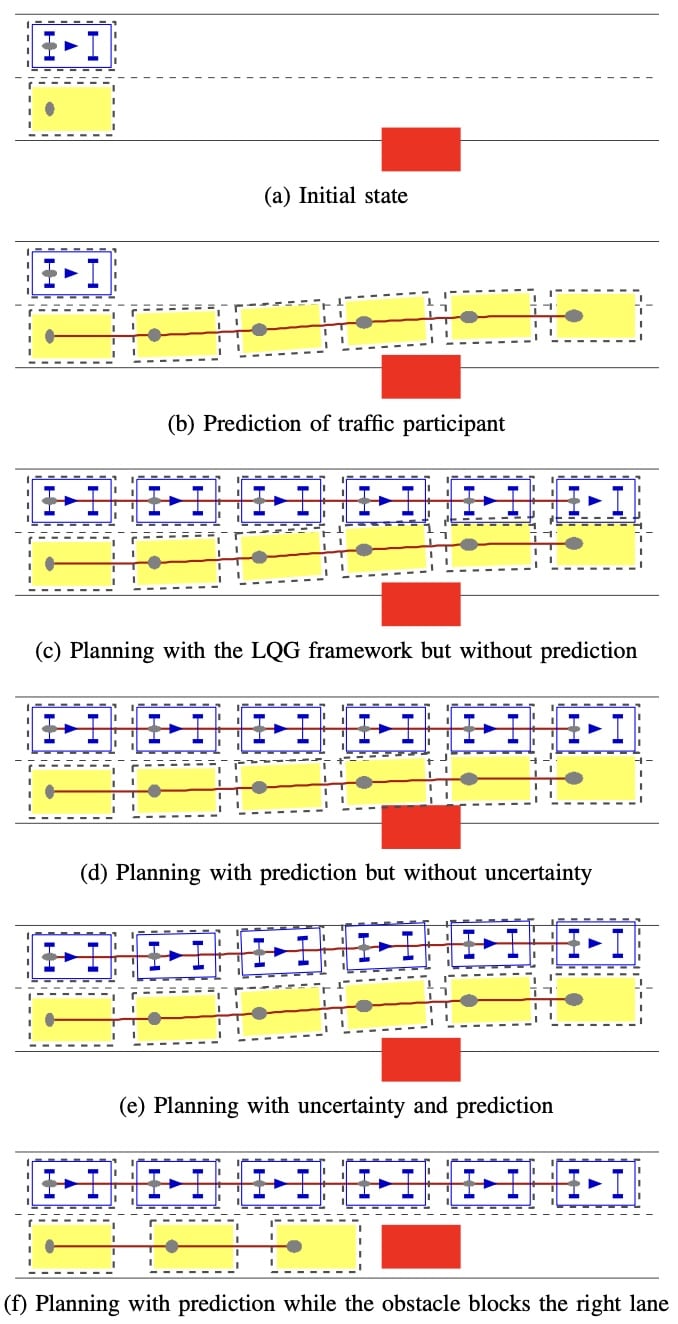
Improvement

一种可能的改进是以更随机的方式预测交通参与者的运动，例如蒙特卡罗模拟。此外，基于意图可以实现更好的预测，这在轨迹历史和现状中揭示。另一个可能的改进是估计比高斯分布更真实的 GPS 误差分布，这将有助于计算对定位不确定性的更好估计。

没有对车辆可能动作估计的解释。

terminology

卡尔曼滤波

可能是讲解最清楚的Kalman filter https://zhuanlan.zhihu.com/p/113685503

图说卡尔曼滤波，一份通俗易懂的教程 https://zhuanlan.zhihu.com/p/39912633

在存在诸多不确定性情况的组合信息中估计动态系统的状态
外部不确定性：我们把这些不确定影响视为协方差 $Q_k$ 的噪声。
两块高斯分布相乘后，我们可以得到它们的重叠部分，这也是会出现最佳估计的区域。

LQR & LQG

优化控制：LQR, LQG https://zhuanlan.zhihu.com/p/136204710

LQG = Linear Quadratic Regulator (理想的线性系统+反馈系统) + 噪声控制

LQG输出调节控制Matlab仿真实例 https://zhuanlan.zhihu.com/p/338340273

通过组合一个最优二次型线性调节器LQR和一个最优状态估计器（卡尔曼滤波器）得到的控制器
虽然系统是”最优“的，但在实际中极易因为建模误差和扰动的存在，导致不稳定。纯粹的LQG并不是一种很实用的控制策略，只适用于简单的、不确定性小的系统。
为了解决LQG的鲁棒稳定性差的问题，有人在LQG的基础上提出了LTR（回路传递恢复）作为补充，通过频域分析，设计闭环零极点位置，从而保证了系统的鲁棒稳定性。也有人干脆放弃LQG，发展出了其他鲁棒控制算法，如H无穷。