Analytical Prediction of Self-organized Traffic Jams as a Function of Increasing ACC Penetration

by Jerath K, Brennan S N. 
from IEEE Transactions on Intelligent Transportation Systems, 2012, 13(4): 1782-1791.

Abstract

background：

ACC 可能改善“人-ACC” 混合的自组织交通拥堵，但是预测“人-ACC” 混合的交通流拥堵发生时刻的closed-form solutions 还不存在。
What we did：

提出了一种封闭形式的解决方案，该解决方案解释了由于自组织交通拥堵（或“幽灵堵车phantom jams”）的形成，以及ACC 对拥堵的影响。

该解决方案利用主方程方法（master equation approach）在细观尺度上对交通流的自组织行为进行建模，并利用通用汽车的第四个跟驰模型在微观尺度上描述驾驶员行为。

研究发现，虽然将启用 ACC 的车辆引入交通流可能会产生更高的交通流，但它也会导致交通流对拥堵的敏感性更高。

Introduction

an increasing mismatch between highway capacity and vehicular population

最近的研究表明，高速公路上的交通拥堵可能是自组织的，即如果车辆密度超过临界值，车辆集群可能会自发地从最初的同质交通中出现。 i.e. vehicle clusters may spontaneously emerge from initially homogeneous traffic if the vehicle density exceeds a critical value

这种没有原因就自己堵上的叫“幽灵堵车”。

使用封闭环形，avoiding unwieldy open boundary conditions such as on- and off-ramps encountered，使得分析amenable （经得起检验）。

Literature Review

设计汽车跟踪或巡航控制算法
目前有关特定巡航控制算法对string稳定性和交通流稳定性的影响的分析结果
宏观模型不利于分析由 ACC 启用和人工驾驶车辆混合组成的交通，而微观模型主要依赖于数值模拟，无法对大量车辆进行解析求解。需要一种中间视角的观察。

Master Equation Approach

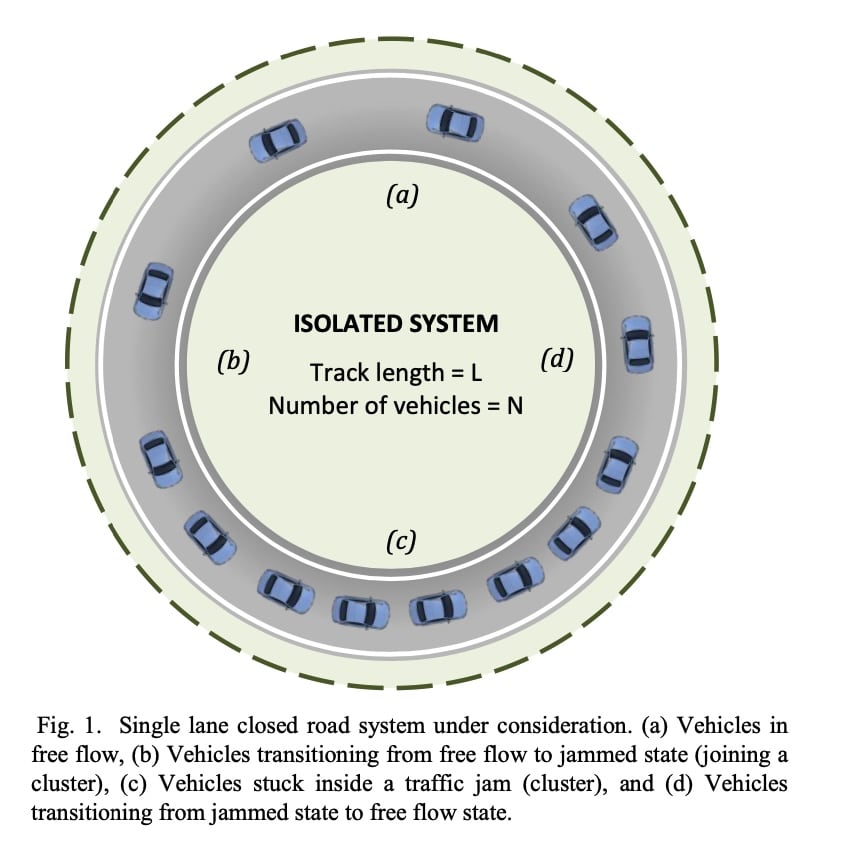
A. Vehicle Cluster (or Traffic Jam) Dynamics

单车道封闭环线路线，车有two states：

the vehicle is in free flow, i.e. it moves independently of any other vehicles on the road, and
the vehicle is stuck in a cluster or traffic jam.

系统的动力学根据状态的概率分布建模为随机过程，使用如下主方程:

$\frac{d}{d t} P(n, t)=\sum_{n^{\prime} \neq n}\left[w\left(n^{\prime}, n\right) P\left(n^{\prime}, t\right)-w\left(n, n^{\prime}\right) P(n, t)\right]$

$w(n^{\prime},n)$ , $w(n,n^{\prime})$ 表示跃迁概率， $P(n^{\prime},t)$ 表示在t 时刻n'拥堵的概率， $P(n,t)$ 表示在t 时刻n拥堵的概率，假设只有单车会加入或离开cluster，状态n 只能转变成相邻的（n-1,n,n+1）方程简化成：

\begin{aligned} \frac{d}{d t} P(n, t)=w(n&-1, n) P(n-1, t) \\ &+w(n+1, n) P(n+1, t) \\ &-\{w(n, n+1)+w(n, n-1)\} P(n, t) \end{aligned}

预期车辆集群规模的动态如下:

\frac{d}{d t}\langle n\rangle=w_{+}\langle n\rangle-w_{-}\langle n\rangle

w+ 表示车辆从自由流动状态到加入一个大小为n的集群并创建一个大小为n+1集群的转移概率，反之亦然。

B. Transition Probability Rates

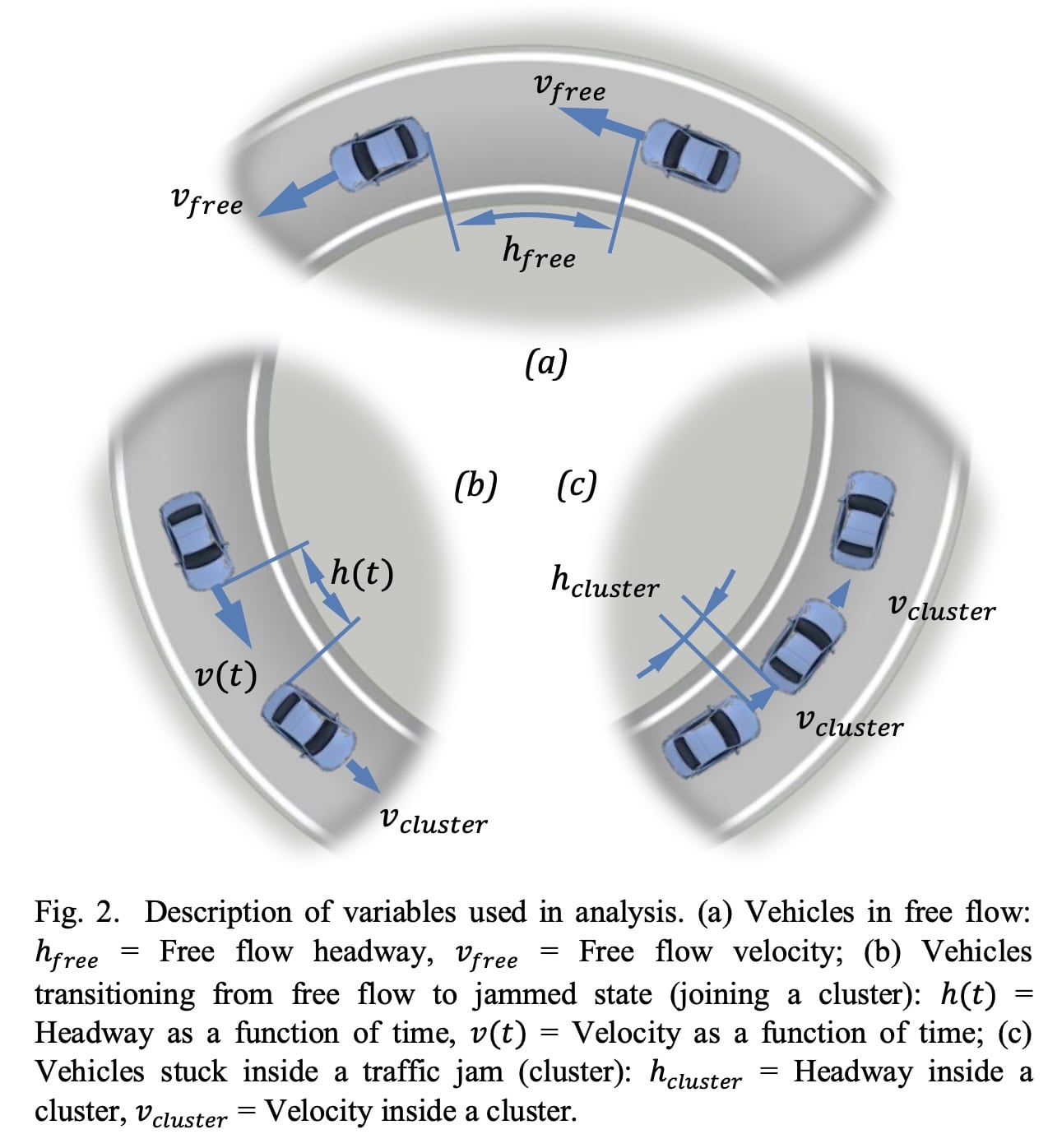
车辆加入规模较大的集群的转移概率被定义为自由流动的车辆加入集群所需时间的倒数，上述方程假设车辆以恒定速度移动并与集群“碰撞”来加入集群，显然不能反应在实际驾驶中的驾驶员保持安全距离的跟驰情况，需要使用一个新的转移概率来更好地反应驾驶员的行为。

新的转换概率率

A. General Motors’ Car-following Model

该模型通过使用三个变量来确定加速控制力：1.前车车距 2.车辆之间的相对速度 3.目标车辆的绝对速度

\ddot{x}_{n+1}(t+\Delta t)=\frac{\alpha\left[\dot{x}_{n+1}(t+\Delta t)\right]}{\left[x_n(t)-x_{n+1}(t)\right]}\left(\dot{x}_n(t)-\dot{x}_{n+1}(t)\right)

$x_{n+1}$ 表示加入集群的车辆位置， $x_n$ 表示前面车辆的位置(或集群中最尾部的车辆)。 $\alpha$ 表示进入集群的车辆的驾驶员的sensitivity (警觉或者困顿)， $\Delta$ t 表示反应时间。

B. Derviation of New Transition Probaility Rates

稳态分析

A. Steady-state Analysis for Single Species Environment

单物种模拟，两种特情况的稳态相图: (I)当⻋辆群仅由人力驾驶⻋辆组成时， (ii)当⻋辆群仅由启用 ACC 的⻋辆组成时。当交通仅由启用 ACC 的⻋辆组成时，交通以更高的临界密度运行，因此交通流量也更高。但是 mesoscopic simulation matches the analytical 结果显示该模拟不能应用于高密度交通流(density p >= 0.8)

多物种混合交通流: 随着道路上ACC 的⻋辆比例增加，临界密度(critical density)增加，并且这种增加不均匀 -> 交通流对⻋辆保有量比例的变化变得越来越敏感。具体来说:左图的两个场景，描绘了交通系统在远离临界密度的相同阈值 delta p下的运行。在无堵塞状态下，以人类驾驶员为主的交通中(A)，⻋辆比例的微小变化不会改变交通流的状态，交通流状态将继续在无堵塞状态下运行。如果在无堵塞状态下(B)以 ACC 为主的交通中引入相同的⻋辆比例变化，它会导致交通流从无堵塞状态变为自组织堵塞或拥塞状态。图12 对于接近峰值流量容量运行的道路，与 ACC 渗透率非常低的交通系统相比，ACC 渗透率非常高的交通系统对自组织交通堵塞造成的拥堵的敏感度高达 10 倍，也就是说:the introduction of a small percentage of human-driven vehicles into a predominantly ACC- enabled vehicle population is more likely to cause a “phantom” traffic jam as compared to the introduction of the same percentage of human-driven vehicles in an already predominantly human-driven vehicle population. (猜测可能是人类驾驶员对高密度情形下的灵活性要大于目前的ACC 算法) 问题和改进空间: 为什么火⻋不会堵⻋? 其中一个很重要的原因是火⻋没法超⻋。显然本文的封闭环形模型为了定量分析没法模拟⻋辆拥堵关于超⻋一最重要因素。不知道将来能不能使用大量的人驾模拟器混合acc算法来模拟真实道路情况，也许在图像和语言识别邻域大量繁重的人工标注工作有一天也会在智能交通领域浮现。

\begin{aligned} & F=(1-p)\left[\frac{\left(f_{v}^{I D M}\right)^{2}}{2}-f_{\Delta v}^{I D M} f_{v}^{I D M} 1-f_{\Delta x}^{I D M}\right]\left[\left(f_{\Delta x}^{I D M}\right)^{-1} f_{\Delta x}^{I D M 2}……f_{\Delta x}^{I D M n} f_{\Delta x}^{C A C C}\right]^{2} \\ & \left.+(1-p) \times p\left[\frac{\left(f_{v}^{I D M 2}\right)^{2}}{2}-f_{\Delta v}^{I D M 2} f_{v}^{I D M 2}-f_{\Delta x}^{I D M 2}\right]\left[f_{\Delta x}^{I D M} 1 f_{\Delta x}^{I D M 2}\right)^{-1} ……f_{\Delta x}^{I D M n} f_{\Delta x}^{C A C C}\right]^{2} \\ \ ……\\ & +\frac{(1-p) \times p^{S+n-1}}{1-p^{S}}\left[\frac{\left(f_{v}^{I D M}\right)^{2}}{2}-f_{\Delta v}^{I D M n} f_{v}^{I D M n}-f_{\Delta x}^{I D M n}\right]\left[f_{\Delta x}^{I D M} f_{\Delta x}^{I D M 2} ……\left(f_{\Delta x}^{I D M n}\right)^{-1} f_{\Delta x}^{C A C C}\right]^{2} \\ \ ……\\ & +\frac{p^{2} \times\left(1-p^{S-1}\right)}{1-p^{S}}\left[\frac{\left(f_{v}^{C A C C}\right)^{2}}{2}-f_{\Delta v}^{C A C C} f_{v}^{\text {CACC }}-f_{\Delta x}^{C A C C}\right]\left[f_{\Delta x}^{I D M 1} f_{\Delta x}^{I D M 2} ……f_{\Delta x}^{I D M n}\left(f_{\Delta x}^{C A C C}\right)^{-1}\right]^{2}<0 \end{aligned}